Hénon Monte Carlo method for
stellar cluster
dynamics
On these pages, we describe biefly a class of numerical schemes used to
follow the long term evolution of
spherically symmetric stellar
clusters. We concentrate on the algorithm invented by Michel
Hénon in the early seventies because it is the inspiration of
all codes presently in use. However, it should be noted that, in the
past, two other, quite different, Monte Carlo (MC) techniques were
developed, by Spitzer et al. and by Shapiro et al (this link).
After the pioneering work of Hénon, his method was adopted and
improved in a variety of directions by Stoldolkiewicz and Giersz in
Warsaw, Joshi, Rasio, Fregeau and Gürkan at the MIT and
Northwestern University and Freitag and Benz at Geneva Observatory and
the ARI in Heidelberg.
There is presently three such codes in use across the world that have
been described in published papers: the "Giersz" MC code, the "MIT/NU"
code and the "Freitag" one. Although all share basic concepts they also
have important differences. Consequently, we start by a presentation of
the common ideas and structures and then present the features specific
to each of them. Follow this link for
references.
In short, the Monte Carlo method borrows both from the N-body
simulations and from methods that treat the stellar cluster as a
contimuum. Like in N-body simulations, the cluster is treated as a set
of reprsentative particles (but they are spherical shells of matter,
not point-masses and their orbital motion is not explicitelly
followed). Like in Fokker-Planck methods, dynamical equilibrium in a
smooth (and spherical) potential is assumed and the secular evolution
of the system (due to relaxation, collisions, stellar evolution,
binaries and/or interaction with a central BH) is investigated. The
treatment of relaxation is based on the same assumptions that underly
the Fokker-Planck equation.
Compared to Fokker-Planck and gaseous methods, the MC scheme, being
particle-based, allows easier and more realistic account of a variety
of physical processes. It is also slower and more noisy. Compared to
the direct N-body methods, it is much faster but more approximate. On a
standard single-processor computer, one can simulate the evolution of a
cluster over a few relaxation times using 0.5 to a few million
particles in a few CPU-days or weeks. The required CPU time scales with
the number of particles N
like N*ln(N) (for a given number of
relaxation times), while the scaling is Nk with k of order 2-3
for direct N-body codes.
Follow the links below for more detailed information.
Physical principles underlying the
Monte Carlo approach.
Numerical implementation.
My MC code, nammed ME(SSY)**2 (Pau's suggestion), is publicly available HERE
Other information on the web.
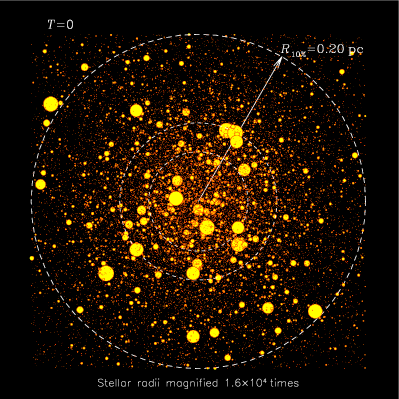
 Evolution of the central region of a spherical
cluster of stars, as computed with the Monte Carlo algorithm. For these
figures, realised for the autumn 2003 issue of inSiDE
newsletter, the angular position of each star on the spherical
shell dealt with by the Monte Carlo code (i.e. a "particle") has been
picked up randomly for the purpose of visualisation. All the stars
within a slice containing the centre are depicted. For clarity, their
radii are highly magnified. The white circles represent spheres
containing 1, 3 and 10% of the total cluster mass. Note how the
massive, large stars concentrate to the centre, through "mass
segregation". See Gürkan,
Freitag & Rasio 04
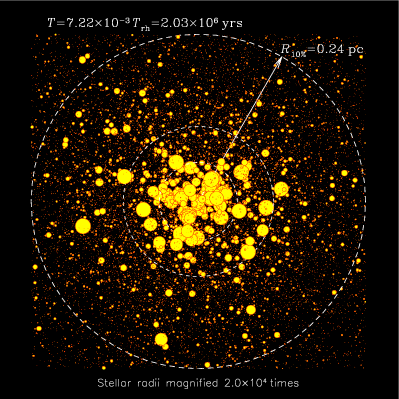
Evolution of the central region of a spherical
cluster of stars, as computed with the Monte Carlo algorithm. For these
figures, realised for the autumn 2003 issue of inSiDE
newsletter, the angular position of each star on the spherical
shell dealt with by the Monte Carlo code (i.e. a "particle") has been
picked up randomly for the purpose of visualisation. All the stars
within a slice containing the centre are depicted. For clarity, their
radii are highly magnified. The white circles represent spheres
containing 1, 3 and 10% of the total cluster mass. Note how the
massive, large stars concentrate to the centre, through "mass
segregation". See Gürkan,
Freitag & Rasio 04
Maintained by Marc Freitag;
comments and contributions welcome. Last Update:
2004-06-01

