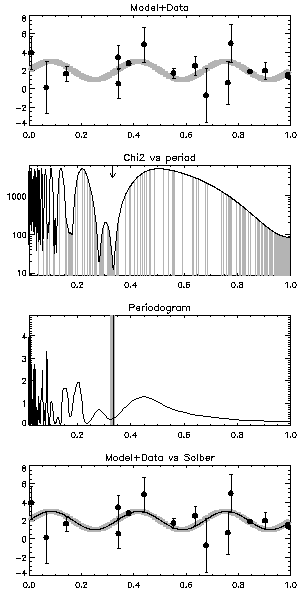
Fitting a sine wave to a poorly/irregularly sampled dataset is a good example of how applying a conventional gradient descent optimization is not always going to return the right answer. Panel 1 of Figure 1 shows the data (black) generated from the model (grey).
From the second panel of Figure 1 it is clear that the chi2 landscape (black curve) has a number of local minima where the solution will get trapped. Initial conditions must be varied to restart the optimizer by hand in the vicinity of each minima.
Solber can sample the parameter space slightly more efficiently than the brute force chi2 minimization. Grey lines in Panel 2 show the locations of intermediate generations of solber models. This picture is typical of GA behavior: the landscape is surveyed in a Monte-Carlo like fashion, but closer attention is paid to the minima encountered.
Of course, there is already a powerful and fast solution to this kind of problem (see e.g. Fast algorithm for spectral analysis of unevenly sampled data). Panel 3 shows Lomb-Scargle periodogram of the data. The location of the highest peak in the spectrum corresponds to the underlying period (grey). This is not very different from the solution found by solber (black).
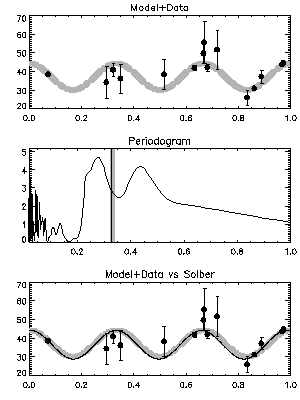
However, highest peak in a periodogram does not always point to the correct period as shown in Figure 2. Here, a valley lies at the location of the underlying period rather than a peak (grey). Solber identifies the period correctly.