PSF Fitting of WFCAM Data: Astrometry
PSF Fitting of WFCAM Data: Astrometry
Document number: VDF-TRE-IOA-00016-0004
Dafydd Wyn Evans, IoA
10 December 2004
1 Introduction
As stated in the previous PSF report ([Evans 2004]), it is intended that the
development of PSF fitting within the WFCAM project
be carried out in 3 phases. This report deals with Phase 2: a list-driven
analysis
with positional updating - this is as in Phase 1, but
the positions are iterated around the given position to determine the best
PSF fit, yielding both photometry and astrometry.
A good paper to read on this topic is [Anderson & King 2000] and a number of ideas are
used from it, especially the use of the effective PSF.
2 The simulations carried out
The source data used in these tests were the same simulations as generated
in [Evans 2003] and used for the previous PSF report.
However, only two sets of simulations were used in these tests:
-
Interleaved data, with all four elements of the interleaved
images generated with the same seeing (0.6").
- Non-interleaved data with the same total integration time as above.
The simulations were carried out down to J=22.2, so that some of the effect of
undetected faint stars could also be accounted for (the detection limit is
about J=20 [Irwin 2003]).
3 Description of general method used
The methodology used is fairly simple with the primary assumptions that:
- All stellar positions down to a limiting magnitude are known.
- The PSF for each star is known.
After a suitably binned PSF is generated for each detected star, a linear
least-squares solution is applied to determine the flux level for these
stars.
Using a list of detected stars (generated by another part of the pipeline),
each star is processed in turn. A cutout is made around the star from the
image data. Then, correctly sampled PSFs are generated for each star within
the cutout that might affect the flux levels. The initial linear
least-squares solution is
generated from this subset of the data and using these PSFs.
The PSFs for the fitting were generated by bilinearly interpolating an
oversampled PSF which was calculated using the data from the whole image. It
was found very early on that using a simple scheme where the required PSFs
were calculated using the nearest neighbour values from an oversampled PSF
was not sufficient, even though the PSFs generated looked reasonable by eye.
This was necessary, not only for determining the PSFs of the primary star in
the solution, but also for the PSFs of the perturbing stars. The background
determination and solution weighting used was as described in the previous
report.
After the initial photometric fit has been carried out, any contaminating
images are removed from the cutout, leaving only the primary image, and a
further fit is carried out to the data. This fit solves for the astrometry
as well as for the photometry and is thus a non-linear one. The method
chosen was the Levenberg-Marquardt method (see [Press et al. 1992]). This requires
the partial differentials of the PSF with respect to X, Y and flux to be
available. This is tabulated at the same time as the measurement of the PSF
as described in the previous report and is computationally fast.
An alternative iterative grid method was tested where no differentials are
used in the fit. Although similar results were found, the code was much
slower.
Also tested was a restriction of the cutout to an aperture of radius twice
the Gaussian sigma of the primary image. This had very little effect on the
simulated data, but performed very poorly with real optical data, possibly
due to the crowded field used. When real data is available from WFCAM more
testing of this aspect will be carried out.
4 Analysis
For photometry, the addition of the non-linear fit does
not improve the accuracy significantly and the results are as reported in
the previous report.
As for photometry, the analysis of the results for the simulated data
is carried out by comparing the true and fitted positions and measuring the
widths of these distributions as a function of magnitude. This will give a
good estimate of the accuracy of the method. This is shown in
Figure 1 for the non-interleaved and interleaved data.
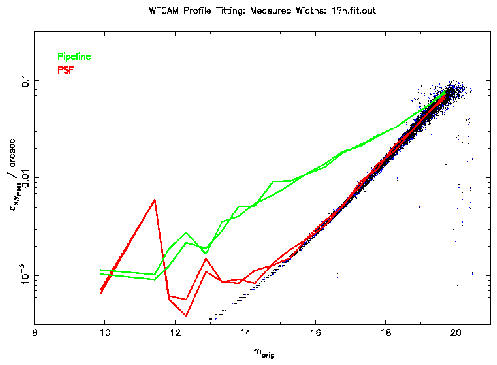
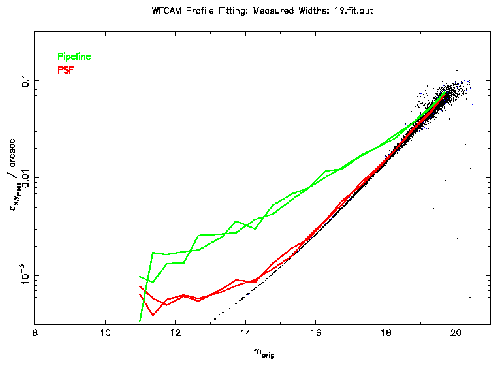
Figure 1: This plot shows the measured astrometric errors for the
non-interleaved and interleaved data. The results for the standard pipeline
astrometry is shown in green and that for the PSF fitting in red. The points
show the formal errors estimated from the PSF fitting.
Also shown is the equivalent error estimation for the default astrometry
generated by the standard CASU pipeline.
In this idealized case, a substantial improvement in accuracies is obtained
by using PSF fitting. Brighter than J=18, the accuracies are a factor of
between 2 and 5 times better.
These plots also show that the error estimation from the fitting process is
in good agreement with that measured. Brighter than J=14-15, the measured
accuracy levels off to 0.8 mas (1/500 pixel) for the non-interleaved data and
0.6 mas (1/300 pixel) for the interleaved data.
This is probably due to limitations in the simulations (roundoff
error etc. ).
Fitting tests were carried out using two different PSF models. The default
model used elliptical Moffat profiles as described in the previous report.
The other model was an adaptive kernel one similar to that used in
[Alard & Lupton 1998]. This model doesn't work quite as well as the one that
uses elliptical Moffat profiles, but this might be expected since the
simulations were carried out using Moffat profiles. Both methods will be
considered for analysing the real data since the adaptive kernel method
might have advantages if the PSF is spatially varying.
5 Speed of code
While carrying out these tests, the processing speed
was noted in comparison with imcore, the standard pipeline programme
for generating image parameters. On average, the determination of the PSF
took about as long as imcore took to process the same file and the
PSF fitting took about 2 to 3 times as long. It should be noted that a lot
of diagnostic calculations are currently carried out in these programmes and
no speed optimization has been attempted.
6 Use of PSF software on optical data
As in the previous report, INT Wide Field Camera data of the
Wolf-Lundmark-Melotte (WLM) galaxy in the Local Group was used to test the
software further. Three frames in each of the passbands Harris V and Sloan
i' were analysed. By using 3 frames it is possible to determine the
external astrometric and photometric errors for each frame by making the
assumption that the width of the residuals in any comparison is equal to the
quadrature sum of the external errors for each frame. With 3 frames it is
possible to generate 3 sets of residuals and thus determine what the
external errors are by solving the simultaneous equations. This also assumes
that the errors are not correlated ie. they are independent. A weakness of
this method is that the measurement of the widths of the distributions is
quite noisy and the nature of the equations amplifies this. Sometimes
solutions are not possible due to this noise. Often 2 frames taken in
similar conditions is enough to determine the external errors by assuming
that they are the same for both frames.
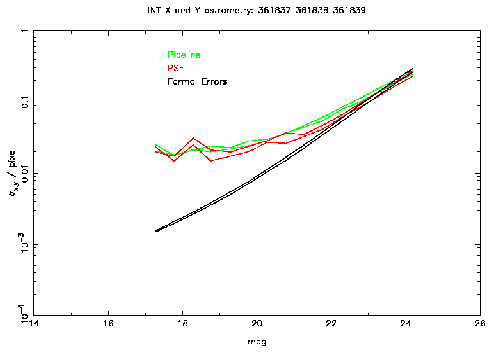
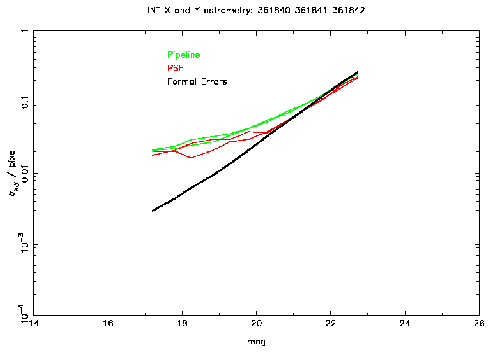
Figure 2: This plot shows the external errors for PSF (red) and
standard pipeline (green)
astrometry as a function of magnitude for data taken with the INT Wide Field
Camera. The V band is on the left and i' on the right. Also shown are the
average formal errors as a function of magnitude (black).
The results shown in Figure 2 indicate that the astrometric
performance of PSF fitting is not very much better than that of the standard
pipeline and certainly doesn't show the marked improvement possible
demonstrated in the simulations (Figure 1). The limit of the
accuracy achieved for this data is 7 mas (1/50 pixel).
Many explanations have been considered to explain what appears to be an
additional, unaccounted for, systematic astrometric error:
- A standard 6-parameter solution is not enough to match the data
between the frames: quadratic terms were added but no improvement was
observed in the accuracies. Similar results were found with radial terms up
to the fourth power. As a test, a comparison was carried out with
only offsets used for the matching and the accuracy limit rose to 30 mas
(1/10 pixel).
- The functional form of the solution used for the frame matching is
inadequate: vector
diagrams of the residuals were investigated and no systematic trends were
visible. This would rule out astigmatism in the corrector as the source of
the error.
- Differential atmospheric refraction: this effect will mainly be in
declination. Between the exposures, the airmass changes from 1.396 to 1.423
(44.25° to 45.35°). For
the V passband, the DR between a B-V of 0.0 and 1.5 will be around
~ 50 mas, thus the maximum size of effect is of order 1 mas and cannot
explain the large errors.
- Varying PSF across the frame: this is unlikely to be the source of the
problem since the pipeline astrometry also seems to be similarly affected.
Also the variation of the χ2 statistic across the field seems to
indicate that this is not a problem (see Section 7).
- Problems with the autoguider: this would result in a shift or a
distortion of the PSF, neither of which would explain the errors seen.
- Crowded field: the exclusion of Extension 4 (the most crowded region)
does not affect the results.
- Chromaticity changes in the corrector: this is highly unlikely since
the telescope is pointing in the same direction and the gravity vector has
only changed by about a degree.
- Pixel phase errors (see [Anderson & King 2000]): this should only
affect undersampled data. However, it was checked and no effect was observed.
- WFC field distortion1: a typical differential of the radial distortion is about 3000 mas over
750 pixels. Since the maximum shift between frames is about half a pixel
this implies a systematic of about 2 mas. Additionally, the 6 parameter fit
will remove a large part of this. Thus, the effect is too small.
- CCD manufacturing inaccuracies: typical pixel tolerances for a CCD is
about 0.5 mm. The WFC pixels are 13.5 mm. Although this is of
the correct order of magnitude to explain the errors,
the images are in the same locations on the CCDs to within a fraction of a
pixel (maximum is half a pixel), thus these errors will be mostly mapped out
since we are considering differential astrometry.
Both PSF models were tested and their performances were again very similar
to each other.
7 The χ2 distribution across the field of view
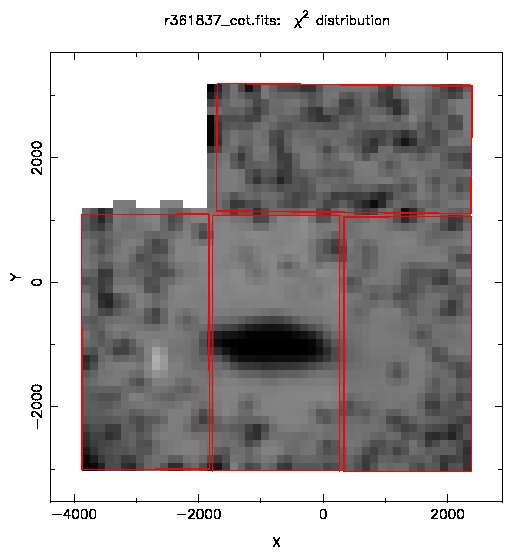
Figure 3: This plot shows the reduced χ2 values across the field of
view of the camera for exposure r361837. Midtone grey corresponds to a value of
1.0.
A Hanning filter (3×3 Bartlett filter) has been applied to the data.
The red outlines show the location of the 4 CCDs.
In order to see if the PSF is varying across the field of view the reduced
χ2 values are plotted as a function of position. These values are
derived from the χ2 values from the PSF fit and are divided by the
number of degrees of freedom. Figure 3 shows the variation for
one of the WLM exposures taken by the INT Wide Field Camera.
The dark region in the centre corresponds to the central parts of the galaxy
and suffers from crowding effects. It is understandable that many of the
images here will be affected by undetected (by the initial pipeline
detection algorithm) images and thus the average PSF will not be a good fit
to the data. Hence the χ2 values for this part of the frame will be high.
Across the rest of the field of view there doesn't seem to be much variation
of the reduced χ2, indicating that the PSF does not vary.
8 Conclusions
The simulations have shown that using PSF fitting can significantly improve
astrometric accuracies. However, tests on optical data show
that these improvements may not be realized.
What is now needed for the further testing of this software is real WFCAM
data taken in good observing conditions.
A postscript version of this report can be found at
http://www.ast.cam.ac.uk/~wfcam/docs/reports/psf2/psf2.ps.
References
- [Alard & Lupton 1998]
-
Alard C., Lupton R.H., 1998, ApJ, 503, 325
`A Method for Optimal Image Subtraction'
- [Anderson & King 2000]
-
Anderson J., King I.R., 2000, PASP, 112, 1360
`Toward High-Precision Astrometry with WFPC2. I. Deriving an Accurate
Point-Spread Function'
- [Evans 2003]
-
Evans D.W., 2003. Internal report
http://www.ast.cam.ac.uk/~wfcam/docs/reports/interleaving/
`Interleaving tests'
- [Evans 2004]
-
Evans D.W., 2004. Internal report
http://www.ast.cam.ac.uk/~wfcam/docs/reports/psf/
`PSF Fitting of WFCAM data'
- [Irwin 2003]
-
Irwin J.M., 2003. Internal report
http://www.ast.cam.ac.uk/~wfcam/docs/reports/simul/#passbands
`WFCAM simulations'
- [Press et al. 1992]
-
Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P., 1992,
Cambridge University Press
`Numerical Recipes in FORTRAN', 2nd edition, page 678
Footnotes:
1See
http://www.ast.cam.ac.uk/ ~ wfcsur/technical/astrometry/
File translated from
TEX
by
TTH,
version 3.30.
On 10 Dec 2004, 18:48.